La influencia de la calidad de los componentes ópticos en la relación señal-ruido del sistema óptico infrarrojo.
- participación
- Tiempo de Publicación
- 2021/12/30
Resumen
En este artículo, Quanhom analiza la influencia de la calidad de los componentes ópticos en la relación señal-ruido de los sistemas ópticos infrarrojos.

Con el desarrollo de la ciencia y la tecnología modernas, se han impuesto requisitos más estrictos para los sistemas ópticos, y las limitaciones de la tecnología de procesamiento y el entorno operativo de los componentes ópticos han causado inevitablemente "defectos" y contaminación de la superficie, como impurezas, rayones y picaduras. . La luz parásita más común en un sistema óptico ingresa al sistema óptico en un ángulo oblicuo fuera del campo de visión, y luego es dispersada en el campo de visión por piezas mecánicas y entra en la ruta óptica posterior. Este tipo de dispersión suele eliminarse fácilmente.
Sin embargo, es mucho más difícil eliminar la luz que incide primero sobre la lente o el espejo y luego se dispersa en el campo de visión por la superficie del elemento óptico para entrar en el campo de visión del sistema óptico. Este tipo de dispersión suele deberse a los dos factores siguientes:
(1) Dispersión causada por rayones, picaduras u otros defectos en la superficie mayores que la longitud de onda de la luz en comparación con la longitud de onda de la luz;
(2) Dado que las superficies ópticas de alta calidad están casi libres de defectos, la dispersión se debe a pequeñas irregularidades en la superficie causadas por el pulido u otros procesos.
En circunstancias normales, debido a las limitaciones de la tecnología de procesamiento moderna, los componentes ópticos inevitablemente dejarán varios defectos en el proceso de procesamiento del sustrato. Además, durante el uso del elemento óptico, su superficie también quedará contaminada.
Este defecto y la contaminación de la superficie provocarán diferentes grados de dispersión de la luz humana, lo que no sólo aumenta la pérdida de energía luminosa, sino que también provoca el deterioro de la calidad de imagen del sistema óptico infrarrojo, lo que a su vez afecta la extracción y análisis de la señal objetivo mediante el sistema óptico infrarrojo. Es necesario estudiar la influencia de los defectos de los componentes ópticos y la contaminación de la superficie en el rendimiento de la radiación parásita del sistema.
Los primeros análisis de radiación parásita de sistemas ópticos infrarrojos se basaban principalmente en la estimación manual de la experiencia. Con el desarrollo de la tecnología informática, surgieron una gran cantidad de programas informáticos de análisis de radiación parásita, incluidos ASAP, Zemax y TracePro. La investigación sobre la contaminación de la superficie de los componentes de sistemas ópticos en el extranjero es relativamente temprana y la literatura se concentra principalmente entre 1980 y 2000. En 1996, AC Terrible del Centro de Vuelo Espacial de la NASA y otros discutieron el impacto de la contaminación de la superficie de los componentes en los equipos espaciales y el control. de la contaminación.
En 1999, Pierre Y. Bely, Matt Lallo del Instituto de Telescopio Espacial NGST (Next Generation Space Telescope) y Keith Parrish del Centro de Vuelo Espacial Goddard llevaron a cabo un análisis de radiación espuria del sistema basado en el proyecto Yardstick y discutieron la contaminación de la superficie de los componentes. de objetos en el rendimiento de radiación parásita del sistema.
La investigación nacional sobre la contaminación superficial de los componentes ópticos comenzó tarde y el trabajo relacionado no es mucho, pero con la atención gradual al problema de la contaminación. También se han logrado algunos avances en la investigación. En 2012, Xiao Jing et al. llevó a cabo un análisis del impacto de la contaminación de la superficie del componente óptico en la relación señal-ruido del sistema, y creyó que cuando la cobertura de las partículas de contaminación de la superficie del componente óptico alcanza un cierto nivel, afectará la detección de señales débiles por parte del sistema óptico.
En 2015, basándose en el modelo de contaminación de cúmulos no uniformes en la superficie del elemento óptico, Wu Jianpeng y otros estudiaron la influencia de la contaminación de los palillos de cúmulos del sistema óptico infrarrojo en las características de radiación parásita del sistema.
Dado un nivel de contaminación de partículas de 300 en la superficie del espejo primario, según la teoría de dispersión de Mie, se analizan cuantitativamente las características de dispersión del sustrato del espejo primario con diferentes niveles de defectos y luego se establece el modelo de dispersión del espejo primario. Sobre esta base, tomando como ejemplo el sistema óptico RC, combinado con el software de análisis óptico ASAP, se simularon y analizaron las características de radiación parásita del sistema de la contaminación moderada en la superficie del espejo principal y su sustrato bajo diferentes niveles de defectos, y Se obtuvieron los correspondientes cálculos de relación señal-ruido.
1. modelo básico
1.1 Modelo de dispersión de Mie
Según el principio de interacción entre luz y materia, cuando un haz de luz ingresa al medio, se producirán una serie de fenómenos físicos como transmisión, refracción y dispersión. Para la dispersión, se puede dividir en dispersión elástica y dispersión inelástica. Para la dispersión elástica, incluye principalmente la dispersión de Rayleigh, la dispersión de Mie y la dispersión no selectiva. Sus características están estrechamente relacionadas con la longitud de onda de la luz incidente, el tamaño, la densidad y la forma de las partículas suspendidas en el agua.
En términos generales, cuando el tamaño de partícula en el medio es mucho menor que la longitud de onda de la onda de luz incidente, la dispersión de Rayleigh se puede utilizar para caracterizar la relación entre la intensidad de la luz dispersada y la longitud de onda de la onda de luz, y cuando el tamaño de partícula es Equivalente a la longitud de onda de la onda de luz, la dispersión de Mie se puede utilizar para la caracterización.
Ya en 1908, Gustav Mie propuso la teoría de la dispersión de la luz al explicar los diversos colores de la luz que se dispersan y absorben por pequeñas partículas coloidales de oro (partículas de sol de oro) suspendidas en agua, que más tarde se denominó teoría de la dispersión de Mie.
Según la teoría de la dispersión de Mie, se puede obtener que la distribución de la intensidad de la luz dispersada de cualquier partícula esférica está estrechamente relacionada con el tamaño y la distribución de la partícula. Para un sistema de partículas con múltiples distribuciones de tamaño de partículas, se puede saber a partir de la teoría de dispersión de Mie que cuando una sola partícula esférica se irradia con una onda plana monocromática con una longitud de onda de λ y una intensidad de luz de I0, la luz dispersada estará encendida. el fotodetector. La energía luminosa dispersada en un anillo es:
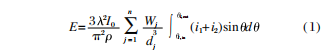
En la fórmula, θ es el ángulo de dispersión; Wj es la masa de la partícula con un diámetro de dj; p es la densidad; i1y yo2son las funciones de intensidad de dispersión, que se pueden expresar como:
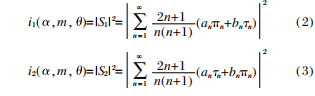
En la fórmula: an y bn son los coeficientes de Michaelis-Men, que son el índice de refracción m de la partícula con respecto al medio circundante y la función del parámetro adimensional α=(πd/λ) que caracteriza el tamaño de la partícula. . La función de Bessel de orden semientero y el segundo tipo de representación de dos números de Hankel; πn y Tn son funciones de ángulo de dispersión, que pueden representarse mediante las funciones de cosθ de Legendre y de Legendre asociadas de primer orden.
Cabe señalar que el valor de n no puede ser demasiado pequeño, de lo contrario el cálculo producirá errores mayores; de manera similar, el valor de n no debe ser demasiado grande; de lo contrario, la convergencia será más lenta y el tiempo de cálculo será mayor. Este artículo se refiere a la fórmula de prueba dada por Wiscombe para determinar el valor efectivo de n.
Para defectos de partículas esféricas, la distribución angular de la intensidad de la luz del campo dispersado se puede obtener a partir de la teoría de dispersión de Mie y luego se puede calcular la dispersión de partículas de diferentes tamaños. Sobre esta base, seleccionando un modelo estadístico apropiado, se puede calcular la dispersión total de los defectos de los componentes ópticos.
1.2 Modelo de relación señal-ruido
Debido a los defectos de los componentes ópticos y la contaminación de la superficie del sistema, el sistema óptico infrarrojo no solo aumentará la radiación térmica de los componentes del sistema al detectar señales débiles, sino que también reducirá la intensidad de la señal objetivo en el campo de ver y aumentar la intensidad de la señal de los objetos fuera del campo de visión, reduciendo así la relación señal-ruido del sistema. Cuando el sistema óptico infrarrojo detecta, el ruido del detector se puede dividir en tres categorías:
(1) El ruido inherente del detector, como el ruido compuesto, el ruido 1/f, el ruido térmico y el ruido de disparo;
(2) El ruido de fotones es el ruido causado por la fluctuación de los electrones fotogenerados generados por la señal y la radiación de fondo, que es proporcional a la 1/2 potencia del número de electrones fotogenerados;
(3) Ruido generado por un amplificador descendente con un determinado ancho de banda de frecuencia, como el ruido de cuantificación.
El cálculo de la relación señal-ruido incluye principalmente el método de tasa de detección de relación y el método electrónico equivalente. El método del electrón equivalente consiste en expresar la señal y el ruido en forma de número de electrones. Convierte la potencia de radiación recibida por la unidad detectora en la cantidad de fotones y luego obtiene la cantidad de electrones a partir de la eficiencia cuántica del detector. El número de electrones equivalente causado por la señal se puede expresar como:
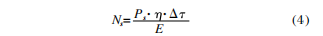
En la fórmula: PS es la intensidad de la señal objetivo; η es la eficiencia cuántica del detector; △T es el tiempo de integración del detector; E = hc / λ es la banda prohibida del detector, h es la constante de Planck y c es la velocidad del vacío de la luz, λ es la longitud de onda de detección.
De la misma forma, el número de fotoelectrones provocados por la potencia de radiación de fondo se puede expresar como:
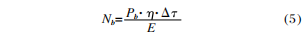
En la fórmula: Pb representa la potencia de radiación de fondo.
En el sistema óptico infrarrojo, para suprimir eficazmente la radiación térmica del propio sistema, el detector suele enfriarse a baja temperatura. Por tanto, el ruido inherente del detector es mucho menor que el ruido de la radiación de fondo. Cuando la potencia de radiación de la señal objetivo es mucho menor que la potencia de radiación de fondo, la relación señal-ruido del sistema óptico infrarrojo se puede expresar como:
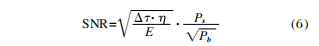
La ecuación (6) muestra que la relación señal-ruido del sistema es proporcional a la potencia de radiación objetivo de la señal e inversamente proporcional a la raíz cuadrada de la radiación de fondo. En general, los detectores de sistemas ópticos infrarrojos suelen estar limitados por el ruido de radiación de fondo cuando detectan señales débiles.
2.Establecimiento del modelo de simulación del sistema y análisis de la relación señal-ruido.
Para estudiar la influencia de la calidad de los componentes ópticos en la relación señal-ruido del sistema óptico infrarrojo, es necesario utilizar el software ASAP para establecer un modelo de simulación optomecánico tridimensional del sistema, y Especifique un modelo de dispersión razonable para cada componente del sistema.
2.1 El establecimiento del modelo de máquina óptica.
Para estudiar el impacto de la contaminación de partículas en la superficie del espejo primario y la replicación de defectos del sustrato en la relación señal-ruido del sistema óptico infrarrojo, se toma como ejemplo el sistema óptico RC. Su estructura se muestra en la Figura 1 y el software de análisis óptico ASAP se utiliza para establecer un modelo de simulación tridimensional.
El ángulo de visión completo del sistema es de 1,6°, el diámetro de la pupila de entrada es de 1200 mm, la banda de ondas de trabajo es de 3-5 μm y la temperatura del sistema es de 275 k. El sistema no tiene una parada en frío 100% compatible para suprimir la radiación de calor de los componentes fuera del campo de visión.
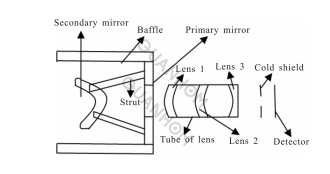
Fig.1 Esquema de diseño del sistema óptico de imágenes infrarrojas.
2.2 Establecimiento del modelo de dispersión.
Una vez establecido el modelo de simulación del sistema óptico infrarrojo, la premisa del análisis de la radiación parásita es especificar el modelo de dispersión apropiado para las partes ópticas y mecánicas del sistema para caracterizar las características de dispersión de su superficie. En el cálculo, se supone que la reflectividad del espejo es 0,98, y se utiliza el modelo de Harvey modificado para describir sus características de dispersión91, y su dispersión total integrada TIS es 0,018%.
La transmitancia de la lente es 0,99 y la dispersión integral total es 0,4%. La reflectividad de las partes mecánicas del sistema es del 2%, y se utiliza el modelo lambertiano con un TIS del 2% para describir sus características de dispersión. La superficie está pintada de negro y la tasa de absorción es 0,96.
Cuando la limpieza de la superficie del elemento óptico es 300, 500, 750 (la cobertura de la superficie de las partículas es 0,03%, 0,3%, 2,7%, respectivamente), corresponde a los tres tipos de contaminación del espejo: contaminación lumínica, contaminación moderada y contaminación intensa. .
La Figura 2 muestra la distribución normalizada de la distribución de dispersión bidireccional (BSDF) con el ángulo de dispersión (Figura 2(a) 300 grados de contaminación de la superficie del espejo, Figura 2(b) 500 grados de contaminación de la superficie del espejo, figura 2(c) 750 grados de contaminación en la superficie del reflector). En un sistema de telescopio grande, el tamaño del espejo primario suele ser mayor y el procesamiento es más difícil.
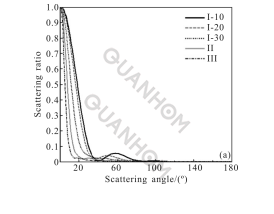
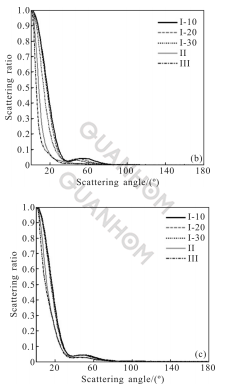
Fig.2 BSDF junto con la distribución normalizada del ángulo de dispersión
Por tanto, este artículo se centra en la investigación sobre la calidad del espejo primario. Tomando como ejemplo el caso en el que la contaminación de la superficie del espejo principal es del nivel 300, las características de dispersión de diferentes niveles de defectos en el sustrato del espejo principal se ajustan con la suma de dos modelos de Harvey modificados para ajustarse a los datos BSDF calculados por el modelo de dispersión de Mie.
La dispersión total del espejo primario es la suma de la rugosidad de la superficie, la contaminación de partículas de la superficie y la replicación de defectos del sustrato. El estándar MIL-STD-1246C se utiliza para aproximar la distribución de partículas para la contaminación por partículas en la superficie del componente. La densidad y el tamaño de las partículas contaminantes obedecen a la distribución log-normal, es decir
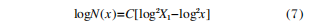
En la fórmula: x es el tamaño de las partículas contaminantes; N(x) es el número de partículas mayores o iguales a x por pie cuadrado; X1es el nivel de limpieza de la superficie del elemento óptico; C es la constante de normalización y el valor de C en este estándar es 0,926. La ecuación (7) muestra que la probabilidad de aparición de partículas de tamaño pequeño es mayor, mientras que la probabilidad de aparición de partículas de gran tamaño es menor. Por lo tanto, en el cálculo, se puede aproximar que las partículas contaminantes en la superficie del elemento óptico son partículas de pequeño tamaño.
En cuanto a los defectos del sustrato, una gran cantidad de experimentos y estudios teóricos han demostrado que el tamaño y la densidad de los defectos de los elementos ópticos obedecen a una distribución exponencial de potencia, es decir, cuanto menor es el tamaño, mayor es la densidad:
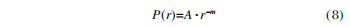
En la fórmula: P representa la densidad cuando el tamaño del defecto es, y A y m son dos parámetros relacionados con elementos ópticos. De acuerdo con los estándares de detección de defectos en la superficie del sustrato en el estándar nacional (GB1185-79), los defectos de los componentes se pueden dividir en 10 niveles de menor a mayor, como I-10, I-20, I-30, II y III. . Alto indica que la calidad de procesamiento del componente es peor.
Para la replicación del defecto del sustrato, el defecto tiene una estructura cilíndrica simétrica con un límite parabólico y su diámetro superficial cumple la siguiente relación con el tamaño y la profundidad de la semilla:
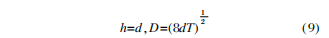
Contenido de muestra
En la fórmula: D es el diámetro del defecto de la superficie de la película; d es el diámetro de la semilla defectuosa del sustrato; T es la profundidad de la semilla. El cálculo supone que el material del sustrato del espejo principal es Si con un índice de refracción de 3,44-2,4 × 10, una sola capa de película de Ag con un espesor de 100 nm está colocada sobre el sustrato de Si y la película protectora es ZnS/YbF3. La longitud de onda calculada es de 4 μm.
Se puede ver en la Figura 2 que la energía de dispersión causada por la contaminación de la superficie del espejo principal y los múltiples efectos de los defectos del sustrato se concentra principalmente en la dirección de avance (el ángulo de dispersión está entre 0°-90°), y cuando Se da el nivel de contaminación de la superficie del espejo principal, el sustrato. Cuanto mayor sea el nivel de defectos, más obvia será la concentración directa y más obvio será el impacto en la replicación de los defectos del sustrato.
Comparando más a fondo las Figuras 2(a)-(c), se puede ver que incluso si la calidad del procesamiento del sustrato es mejor, si la contaminación de la superficie del elemento óptico es más grave, mayor será la cantidad de dispersión que causa. Por el contrario, incluso si la superficie del elemento óptico está ligeramente contaminada, si la calidad del procesamiento del sustrato es peor, la cantidad de dispersión también es mayor.
2.3 Análisis de la relación señal-ruido
Dado que la relación señal-ruido está relacionada con la radiación de la señal y la radiación de fondo recibida por el detector, es necesario analizar las características de la radiación parásita del sistema óptico infrarrojo. La radiación de fondo que recibe el detector incluye la radiación térmica de los componentes internos del sistema y la radiación parásita de fuentes de radiación externas. Entre ellas, las fuentes externas de radiación parásita incluyen principalmente el sol y el fondo del cielo.
2.3.1 Radiación térmica de los componentes internos del sistema.
En el caso de que la contaminación de la superficie del espejo principal sea de nivel 300, tome como ejemplo el telescopio RC que se muestra en la Figura 1, los defectos del sustrato del espejo principal son respectivamente I-10, I-20, I-30, I y II, y el espejo principal El análisis preliminar de seis condiciones de limpieza (es decir, sin defectos en el sustrato y sin contaminación en la superficie del espejo principal) encontró que la suma del flujo de radiación parásita de las partes mecánicas en el sistema es mayor que la suma del flujo de radiación parásita de las partes ópticas. Optimice de la siguiente manera:
(1) Se agregó un anillo de bloqueo de luz al capó del sistema;
(2) Ennegrecer las piezas mecánicas que no sean críticas;
(3) Para el cilindro de la lente, etc., que son la superficie clave pero no la superficie irradiada, áselo;
(3) Para las nervaduras de soporte, etc., que son tanto la superficie clave como la superficie irradiada, primero ennegrezcalas y luego déjelas ásperas. La Tabla 1 muestra el flujo de radiación parásita de cada elemento del sistema óptico infrarrojo que llega al plano de imagen del detector.
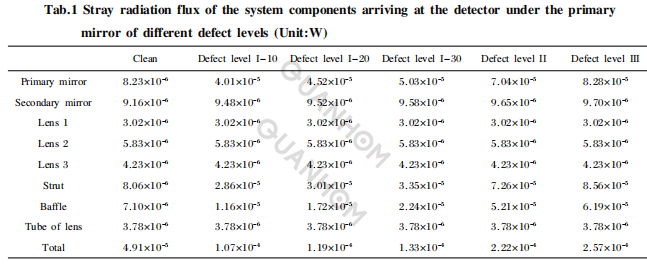
Se puede ver en la Tabla 1: En el caso de una contaminación de la superficie del espejo primario dada de 300 niveles, con el aumento del nivel de defecto del sustrato del espejo primario, el flujo de radiación parásita del espejo primario aumentará con el aumento de su propia emisividad. Aumentar. El flujo de radiación parásita del espejo secundario básicamente no cambia. La razón principal es que el espejo secundario está frente al detector y su propia radiación de cadmio perdida puede llegar directamente al detector, por lo que se ve menos afectado por el defecto del sustrato del espejo primario.
Casi no hay cambios en el flujo de radiación parásita de las tres lentes y el cilindro de la lente, principalmente porque este elemento está ubicado en el grupo trasero del sistema, y su propia radiación parásita no necesita ser reflejada ni dispersada por los lentes primario y espejos secundarios. El flujo de radiación parásita de las nervaduras de soporte y del capó aumentará con el aumento de la cantidad de dispersión en la superficie del espejo primario. La razón principal es que la radiación parásita de las piezas mecánicas ingresa en el camino óptico posterior a través de la dispersión de los espejos primario y secundario y finalmente llega al detector.
2.3.2 Análisis de las características de la radiación parásita de fuentes de radiación externas
Generalmente, la radiación solar no puede alcanzar directamente el plano de imagen del sistema y su radiación dispersa sólo puede llegar al detector a través de la dispersión de los componentes internos del sistema. Dado que el sistema óptico generalmente no detecta el objetivo directamente, se supone que los ángulos entre la luz incidente del sol y el eje óptico del sistema son de 10°, 20° y 30° respectivamente, y el sol se considera como un Cuerpo negro con una temperatura de 5900K.
El fondo del cielo llega principalmente al plano focal del detector a través del reflejo de los espejos primario y secundario. Al analizar las características de la radiación parásita del fondo del cielo, el fondo del cielo equivale a un cuerpo negro de 200-280K. La contaminación en la superficie del espejo primario está en el nivel 300, cuando el espejo principal tiene diferentes niveles de defectos y el espejo principal es ideal, el flujo de radiación parásita del sol y el fondo del cielo recibido por el detector se da en la Tabla 2 con un Longitud de onda de 3-5 μm.
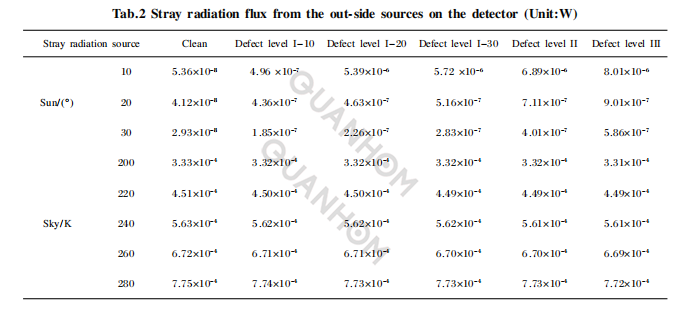
Puede verse en la Tabla 2 que el flujo de radiación parásita solar recibido por el detector es menor que el flujo de radiación parásita del fondo del cielo. Además, cuando la contaminación de la superficie del espejo principal es del nivel 300, cuando el ángulo de incidencia del sol y el eje óptico del sistema es constante, el flujo de radiación parásita solar recibido por el detector aumentará significativamente con el aumento del defecto. nivel del sustrato del espejo principal.
La razón principal es que cuanto mayor es el nivel del defecto del sustrato, mayor es la cantidad de dispersión en la superficie del componente y mayor es la energía de la radiación solar que eventualmente es dispersada por el espejo y llega al detector.
Cuando el nivel de defecto del sustrato del espejo principal es constante, a medida que aumenta el ángulo de incidencia del sol y el eje óptico del sistema, el flujo de radiación parásita solar recibido por el detector disminuye gradualmente.
Cuando la temperatura de fondo del cielo no cambia, el flujo de radiación parásita de diferentes niveles de defectos del sustrato del espejo principal disminuirá gradualmente a medida que disminuye la transmitancia del sistema, pero el cambio no es significativo. Cuando la temperatura de radiación efectiva del fondo del cielo cambia entre 200 y 280 k, el flujo de radiación parásita del fondo del cielo recogido por el detector aumentará gradualmente con el aumento de su temperatura de radiación.
2.3.3 Análisis de la relación señal-ruido
Se puede ver en las Tablas 1 y 2 que la radiación solar recibida por el detector es menor que el fondo del cielo y la radiación térmica de los componentes internos del sistema. Por lo tanto, al analizar la influencia de la contaminación de la superficie del espejo principal y los diferentes niveles de defectos del sustrato en la relación señal-ruido, solo la radiación solar discute la situación cuando el ángulo entre el haz humano y el eje óptico del sistema es 30 °. La ecuación (6) muestra que la relación señal-ruido del sistema está relacionada con la radiación de la señal y la radiación de fondo recibida por el detector.
La radiación de fondo que recibe el detector es la suma de la radiación térmica de los componentes internos del sistema y la radiación parásita del sol y del cielo. El cambio relativo en la relación señal-ruido causado por la contaminación y los defectos del elemento óptico sólo está relacionado con la magnitud relativa de la señal y la radiación de fondo, pero no con la relación señal-ruido inicial cuando el elemento óptico esta limpio.
Para analizar de manera cómoda e intuitiva la influencia relativa de la contaminación del espejo en la relación señal-ruido, la relación señal-ruido cuando la superficie del espejo está limpia con diferentes temperaturas de radiación de fondo del cielo se establece en 1, para obtener la intensidad de la señal objetivo para cálculos posteriores.
Los parámetros utilizados para calcular la relación señal-ruido son: △T=1X10, η=0,5, E=1,7x10J. La Tabla 3 muestra el valor relativo de la relación señal-ruido al replicar defectos con diferentes temperaturas de radiación en el fondo del cielo y diferentes niveles de defectos en el sustrato del espejo principal.
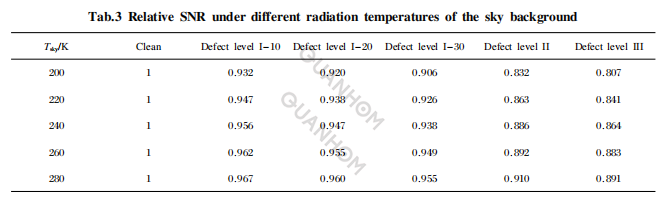
Al analizar la Tabla 3, se puede ver que dada una contaminación de nivel 300 en la superficie del espejo primario, la relación señal-ruido se reduce significativamente a medida que aumenta el nivel de defecto del sustrato del espejo primario. Además, cuando el nivel de defectos del sustrato del espejo principal permanece sin cambios, a medida que aumenta la temperatura de radiación de fondo del cielo, la influencia de la contaminación en la superficie del espejo principal y los diferentes niveles de defectos del sustrato en la relación señal-ruido la proporción disminuye gradualmente.
2.3.4 Discusión sobre la tolerancia de los componentes ópticos del sistema.
Durante el funcionamiento del sistema óptico infrarrojo, cuando la contaminación en la superficie del elemento óptico y el nivel de defecto del sustrato están dentro de un cierto rango, el rendimiento de detección del sistema se puede considerar básicamente sin cambios, y cuando el nivel del espejo La contaminación y los defectos del sustrato exceden este límite, el rendimiento de detección del sistema disminuye rápidamente y el rango permitido de niveles de contaminación y defectos es la tolerancia a la contaminación del sistema.
Para los sistemas ópticos infrarrojos, la tolerancia a la contaminación de los componentes ópticos se puede definir como: el cambio relativo de la relación señal-ruido antes y después de la contaminación debe controlarse en aproximadamente un 10% para garantizar una detección efectiva de señales débiles cuando la señal- La relación ruido es baja.
Para garantizar el rendimiento de detección del sistema, es decir, el cambio en la relación señal-ruido causado por la contaminación y los defectos no puede ser superior al 10%. Según el cálculo de simulación en la sección 2.3.3, se puede saber que cuando la contaminación de la superficie del espejo principal se da en el nivel 300, cuando el sustrato es defectuoso es Clase II, y la reducción relativa de la señal a- la relación de ruido cuando la temperatura de fondo del cielo es inferior a 280 K ha superado el 10 %.
En este momento, dada una contaminación de nivel 300 en la superficie del espejo primario, para garantizar el rendimiento de detección del sistema, el nivel de defectos en los componentes ópticos debe controlarse estrictamente dentro del nivel II.
Además, en aplicaciones prácticas, es necesario reducir aún más el impacto de la contaminación por partículas de los componentes ópticos en la relación señal-ruido del sistema mediante el seguimiento y control de la contaminación. En primer lugar, se utilizan diferentes métodos de detección de contaminación para componentes ópticos con diferentes tolerancias a la contaminación. Para la superficie del componente con un alto grado de tolerancia a la contaminación, una vez que se observe que el componente está sucio, límpielo y déle mantenimiento.
Para algunas superficies con requisitos de limpieza más estrictos, se puede colocar cerca una plantilla de seguimiento similar. La supervisión en línea de la superficie del componente se puede realizar a través de la plantilla de supervisión. Cuando se descubre que la limpieza está por debajo del rango aceptable, la muestra de monitoreo y los componentes contaminados deben limpiarse al mismo tiempo.
En segundo lugar, se deben seleccionar buenas condiciones ambientales durante la observación y se debe minimizar el tiempo de exposición de la superficie del componente tanto como sea posible. Durante la operación del sistema, se deben evitar las fuentes de contaminación molecular, como la contaminación por partículas y la contaminación por petróleo, y los trabajadores deben cumplir con las pautas de contaminación pertinentes antes y después de ingresar al área de control de la contaminación.
Para reducir o incluso erradicar la contaminación de la superficie de los componentes desde su origen, es necesario tomar medidas de prevención a partir de los siguientes aspectos. En primer lugar, en el diseño del sistema, los componentes sensibles a la contaminación deben mantenerse lo más alejados posible de la fuente de contaminación, de modo que la fuente de contaminación no pueda "ver" directamente la superficie clave. En segundo lugar, al seleccionar los materiales componentes, se deben verificar de antemano las características y la tecnología de procesamiento de los materiales a seleccionar.
Además, se debe controlar la limpieza de la superficie del componente durante todo el proceso de ensamblaje del sistema y se debe minimizar el tiempo de exposición de la superficie del componente.
Finalmente, se deben tomar medidas de cobertura durante el transporte y durante la inactividad. Además, una vez que se descubre que el nivel de contaminación de la superficie del componente excede la tolerancia, se deben tomar medidas para limpiar la superficie del componente. Por ejemplo, el uso de métodos de limpieza sin contacto, como la pulverización de líquido, puede controlar la limpieza de la superficie del componente limpio dentro del nivel 250 (la cobertura superficial de partículas contaminadas en el componente es aproximadamente 0,01%).
3. Conclusión
Sobre la base de la teoría de dispersión del medidor, utilizando el modelo de contaminación de partículas y el modelo estadístico de la distribución de defectos del sustrato, se analizan las características de dispersión de los elementos ópticos con diferentes niveles de defectos en el sustrato cuando la contaminación de la superficie del espejo principal es del nivel 300. y se establece el modelo de dispersión.
Finalmente, tomando como ejemplo el sistema de telescopio RC, se calcula la influencia en la relación señal-ruido. Dado que la contaminación superficial de un determinado componente es 300, el estudio muestra que:
(1) Con el aumento del nivel de defectos del sustrato del espejo principal, la cantidad de dispersión aumenta gradualmente, y cuanto mayor es el nivel de defectos del sustrato del espejo principal, más obvia es la concentración directa, por lo que mayor es el nivel de defectos del sustrato del espejo principal, el efecto de replicación del impacto es más obvio;
(2) El análisis de radiación térmica del sistema de telescopio RC muestra que para el espejo primario, el espejo secundario y el espejo de soporte del elemento en el campo de visión, la dispersión.
El flujo radiante no cambia mucho, pero para el anillo del espejo primario, el anillo del espejo secundario y la armadura de los elementos fuera del campo de visión, la radiación parásita aumentará rápidamente a medida que aumenta la cantidad de dispersión en la superficie del espejo primario;
(3) El análisis de las características de la radiación parásita externa del sol muestra que con el aumento del nivel de defecto del sustrato del espejo principal, el flujo de radiación parásita solar recibido por el detector aumenta significativamente.
(4) El análisis de las características de la radiación parásita externa del fondo del cielo muestra que cuando la temperatura del fondo del cielo no cambia, el flujo de radiación parásita disminuye ligeramente con el aumento del nivel de defecto del sustrato del espejo principal. Cuando la temperatura de radiación efectiva del fondo del cielo cambia entre 200 y 280 K, el flujo de radiación parásita del fondo del cielo recibido por el detector aumentará gradualmente con el aumento de su temperatura de radiación;
(5) El análisis de la relación señal-ruido del sistema muestra que cuando la temperatura de radiación del fondo del cielo es constante, la relación señal-ruido disminuye gradualmente con el aumento del nivel de defecto del sustrato del espejo principal. Además, cuando el nivel de defectos del sustrato del espejo principal permanece sin cambios, a medida que aumenta la temperatura de radiación del fondo del cielo, la influencia de los diferentes niveles de defectos del sustrato del espejo principal en la relación señal-ruido disminuye gradualmente;
(6) El análisis de tolerancia de los componentes ópticos del sistema muestra que el nivel de defectos en los componentes ópticos debe controlarse estrictamente dentro del nivel II. Por lo tanto, en aplicaciones prácticas, es necesario controlar estrictamente el nivel de contaminación de la superficie del elemento óptico y el nivel de defectos de la superficie del sustrato para garantizar que el rendimiento del sistema óptico infrarrojo satisfaga la demanda.
Como experto en la investigación de lentes ópticas infrarrojas durante muchos años, Quanhom puede brindarle opiniones de orientación profesional en gran medida en diferentes lugares.
Como fabricante experimentado de componentes optoelectromecánicos, Quanhom está equipado con un sistema de inspección de calidad profesional y un equipo de gestión integral y disfruta de una gran reputación en la industria. Nuestros productos se venden en todo el mundo y se utilizan en todos los ámbitos de la vida. Nuestro atento servicio de ventanilla única también ha recibido elogios unánimes de los clientes. Si está interesado en nuestras lentes ópticas infrarrojas, ¡contáctenos de inmediato!
Autor: Tú Xinghai, Zhang Bin
Fuente de la revista: Vol.47 No.3 Ingeniería láser e infrarroja, marzo de 2018
Manuscrito recibido: 2017-10-05, fecha de revisión: 2017-11-15
Referencias
[1] Jiang Lun, Hu Yuan, Dong Keyan y otros. Diseño atérmico pasivo del sistema óptico infrarrojo de doble banda [J]. Ingeniería de infrarrojos y láser, 2015,44(11): 3353-3357. (en chino)
[2] Facey TA, Nonnenmacher A L. Medición de la emisividad hemisférica total de superficies de espejos contaminadas [C]//SPIE, 1989, 967: 308-313.
[3] Spyak PR, Wolfe W L. Dispersión de espejos contaminados con partículas. Parte 1: teoría y experimento para esferas de poliestireno y =0,632 8 [J]. Ingeniería óptica, 1992,31(8): 1746-1756.
[4] MIL-STD-1246C. (15 de febrero de 2002) [S]. Programa de control de contaminación y niveles de limpieza de productos estándar militar, 2002.
[5] Li Fangqing, Zhang Bin, Xiao Jing, et al. Análisis de luz parásita del espejo contaminado del sistema óptico infrarrojo[J]. Óptica y tecnología optoelectrónica, 2010, 8(4): 22-25. (en chino)
[6] Pierre Y Bely, Matt Lallo, Larry Petro. Análisis de luz parásita de la misión de medición [DB/OL]. [1999 -07 -23].http://www.ngst.stsciedu/nms/main/repo.
[7] Tribble AC, Boyadjian B, Davis J, et al. Directrices de diseño de ingeniería de control de la contaminación para la comunidad aeroespacial [R]. Alabama, Centro Marshall de vuelos espaciales: Informe del contratista de la NASA, 1996: 4740.
[8] Él P, Xiao J, Zhang B, et al. La influencia del espejo contaminado en las distribuciones de flujo de radiación parásita de los sistemas de telescopios infrarrojos [C]//SPIE, 2010, 7654: 76540T.
[9] Xiao Jing, Zhang Bin. Influencia de la contaminación de los componentes ópticos en la relación señal/ruido en sistemas ópticos infrarrojos [J]. Ingeniería de infrarrojos y láser, 2012, 41 (4): 1010-1016. (en chino)
[10] Wu Jianpeng, Luo Wenfei, Peng Jiaqi y otros. Influencia de la contaminación de grupos de partículas en la radiación de luz parásita de sistemas ópticos infrarrojos [J]. Revista de la Universidad de Sichuan (Edición de Ciencias de la Ingeniería), 2010, 8(4): 22-25. (en chino)
[11] Dave J V. Dispersión de la luz visible por grandes esferas de agua [J]. Óptica Aplicada, 1969, 8(1): 155-164.
[12] Zhang Wei, Lu Yuan, Du Shiming y otros. Análisis de las características de la dispersión de Mie [J]. Técnica óptica, 2010, 36(6): 936-939. (en chino)
[13] Wang Xueyan. Investigación sobre el algoritmo de prueba de tamaño de partículas basado en la teoría de Mie [D]. Universidad Tecnológica de An, 2011. (en chino)
[14] Craig F. Bohren, Donald R. Huffman. Absorción y dispersión de luz por partículas pequeñas [M]. Estados Unidos: John Wiley & Sons, Inc., 1998: 234-288.
[15]Aikens DM, Wolfe CR, Lawson J K. El uso de funciones de densidad espectral de potencia (PSD) para especificar la óptica para la Instalación Nacional de Ignición[C]//SPIE, 1995, 2576: 281-292.
[16] Yan Peipei, Fan Xuewu. Diseño óptico y análisis de luz parásita del sistema R-C [J]. Tecnología Infrarroja, 2011, 33(4): 214-218. (en chino)
[17] Zhou Lidan. Investigación sobre la ley estadística entre la distribución de "defectos" de componentes ópticos y la calidad del campo nea en un sistema láser de alta potencia [D]. Mianyang: Academia China de Ingeniería Física, 2009 (en chino)
[18] Usted Xinghai, Hu Xiaochuan, Peng Jiaqi, et al. Efecto de los defectos del componente sobre las características de la radiación parásita del sistema óptico infrarrojo [J]. Ingeniería de infrarrojos y láser, 2017, 46(1): 0120004. (en chino)
[19] Xu Deyan, Wang Qing, Gao Zhishan y otros. Detección de componentes ópticos actuales y estándares internacionales [M]. Beijing: Science Press, 2009: 264-267. (en chino)
[20] Shan Yongguang, Liu Xiaofeng, He Hongbo y otros. Avances de la investigación del defecto nodular en recubrimientos ópticos [J]. Láser de alta potencia y haces de partículas, 2011, 23(6): 1421-1429 (en chino).
[21] Tribble AC, Boyadjian B, Davis J, et al. Pautas de diseño de ingeniería de control de contaminación para la comunidad aeroespacial Informe del contratista de la NASA [R]. Alabama: Centro Marshall de vuelos espaciales, 1996: 4740.
[22] Chen PT, Hedgeland RJ, Thomson S R. Acomodación superficial de contaminantes moleculares [C] // Contaminación del sistema óptico: efectos, medición, control II. Sociedad Internacional de Óptica y Fotónica, 1990: 327-336.
[23] Vest CE, Buch RM, Lenkevich M J. Selección de materiales en relación con la contaminación de las superficies de las naves espaciales [J]. Sampe trimestral, 1988, 19(2): 29-35.
[24] Lei Min, Li Xiaoping, Miao Huaikun. Desarrollo de técnicas de control de contaminación para superficies ópticas EUV [J]. Progreso del láser y la optoelectrónica, 2013, 50 (3): 030005. (en chino)