¿Cómo juzgan los diseñadores ópticos el rendimiento de las lentes ópticas?
- participación
- Tiempo de Publicación
- 2022/5/20
Resumen
Si bien los gráficos de aberración son buenos para proporcionarle al diseñador óptico el rendimiento de una lente, generalmente son un criterio objetivo para el usuario o evaluador de la lente. El siguiente artículo describe brevemente el método del diseñador óptico para determinar el rendimiento de una lente óptica.

Si bien los gráficos de aberración son excelentes para proporcionarle al diseñador óptico el rendimiento de una lente, generalmente, especialmente para el usuario o evaluador de la lente, es muy necesario un estándar objetivo.
La función de transferencia de modulación (MTF) es uno de los criterios más utilizados para la evaluación de imágenes de luz incoherente, donde la atención se centra en el contraste o la nitidez de la imagen.
De hecho, muchas lentes ópticas modernas se miden directamente según el rendimiento del MTF.
Como se muestra en la Figura 1, considere un sistema óptico que genera imágenes de una rejilla con una distribución de intensidad sinusoidal. Para imágenes con luz incoherente, la intensidad de la imagen también es sinusoidal, pero el contraste se reduce.
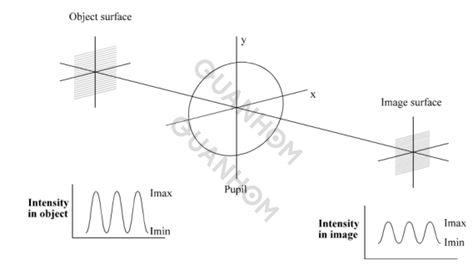
Figura 1 Comparación de imágenes de objetos de un sistema óptico.
MTF es el contraste de la imagen dividido por el contraste del objeto; obviamente, es una función de la frecuencia espacial, y los gráficos de MTF en función de la frecuencia espacial (normalmente en "pares de líneas/mm") se utilizan a menudo en el diseño óptico.
La función de transferencia óptica se define como:

Estrictamente hablando, debemos distinguir entre función de transferencia óptica (OTF) y función de transferencia de modulación (MTF).
El OTF es un vector que incluye la fase y amplitud de la imagen, donde la amplitud es el MTF.
De hecho, la principal consideración en el diseño óptico es el MTF. El término de fase, a veces denominado función de transferencia de fase (PTF), representa la desviación de la imagen sinusoidal real de la imagen sinusoidal ideal, expresada en función del ángulo de fase en función de la frecuencia espacial. Si la fase excede los 180°, el MTF puede ser negativo. Esto representa una inversión de fase, lo que resulta en una inversión del contraste de la imagen. En realidad, esto puede ocurrir en las altas frecuencias de muchas lentes.
1. Teoría
Para sistemas iluminados por luz incoherente, la MTF se puede obtener utilizando la transformada de Fourier de la función de dispersión de línea. Normalmente, el MTF se obtiene de esta forma.
Sin embargo, la difracción OTF se puede resolver rápidamente mediante la integración de autocorrelación:
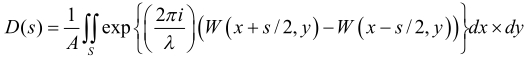
donde D(s)=OTF, A=área de la pupila de luz, S es el área de superposición de las dos pupilas de luz, W es la aberración del frente de onda, S es la frecuencia espacial simplificada igual a fλ/NA y NA es la apertura numérica.
2. Aproximación geométrica
En la aproximación de óptica geométrica, asumimos que λ está cerca de cero, por lo que la MTF (en la dirección Meridional) es:
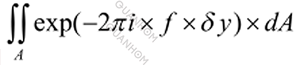
Se trata de la integración de todo el alumno, que en la práctica puede aproximarse mediante una simple suma.
3. La solución real
Debido a que necesitamos conocer no solo la dirección sagital sino también la MTF en la dirección meridional, la MTF en la dirección sagital se resuelve mediante la siguiente fórmula:
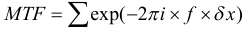
La MTF en la dirección del meridiano se obtiene mediante la siguiente fórmula:
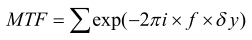
Es conveniente rastrear numerosos (a menudo más de 100) rayos de luz, pero para el cálculo de la suma sólo se consideran los rayos que realmente pasan a través del sistema. También rastreamos rayos de múltiples longitudes de onda, y las longitudes de onda se pueden ponderar de manera diferente al sumar. Es fácil agregar un factor de corrección a la MTF geométrica multiplicando la MTF geométrica por la MTF de difracción del sistema ideal. Este resultado permite que la MTF geométrica sea precisa tanto en sistemas de aberración grande como en sistemas de aberración pequeña.
Sin embargo, para aberraciones moderadas, la MTF geométrica suele dar resultados decepcionantes. Ahora tenemos que decidir cuántos rayos anulares rastrear. Tomando los rayos de la forma que se muestra en la Figura 2, se puede ver que las áreas de todas las áreas pequeñas del semicírculo son iguales. Es fácil ver que si hay n anillos de rayos, el número total de rayos es 2n. Cuando el sistema óptico es simétrico (simétrico con respecto al plano y del meridiano), para ahorrar tiempo, el programa no necesita calcular los rayos en la dirección x negativa.
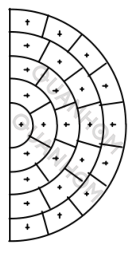
Figura 2. Método de toma de líneas para calcular el MTF geométrico
4. Límite de difracción
Cuando una lente con una apertura de pupila finita forma imágenes de un objeto sinusoidal, la frecuencia límite de su difracción MTF es:
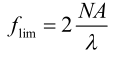
Por ejemplo, para una lente f/2 con una apertura numérica NA de 0,25, cuando la longitud de onda λ es 0,0005 mm, la frecuencia de corte es:
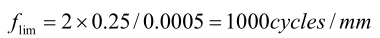
Esta frecuencia corresponde a una rejilla con un período espacial de 0,001 mm (1 μm), pero tenga en cuenta que el valor de MTF correspondiente a esta frecuencia es cero. Para 500/ciclos mm, el MTF de una lente ideal es aproximadamente del 40%, por lo que f/2 es una frecuencia más realista.
5. MTF en ZEMAX
El MTF utilizado en ZEMAX funciona como herramienta de evaluación y como herramienta de optimización.
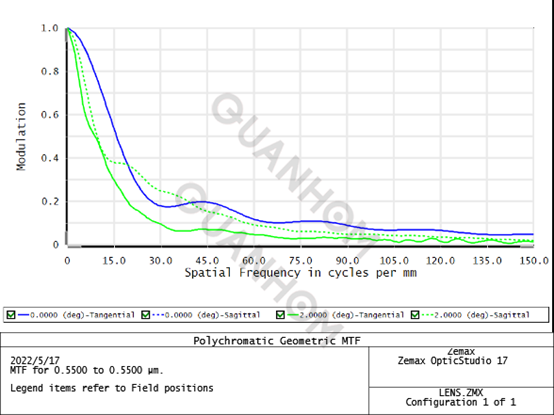
En la figura anterior, hay en total cuatro curvas, de las cuales dos son curvas meridionales MTF y las otras dos son curvas sagitales MTF. En el campo de visión de 0°, la curva MTF meridional y la curva MTF sagital coinciden; y en el campo de visión de 2°, la curva MTF meridional y la curva MTF sagital son bastante diferentes. Esto se debe a que el PSF se vuelve asimétrico cuando está fuera de eje, lo que resulta en una diferencia en el ancho y el perfil del PSF junto con las direcciones meridional y sagital. Por tanto, la convolución con la imagen paraxial (o geométrica) dará como resultado un delta en ambas direcciones. Esto también significa que la resolución es diferente en estas dos direcciones.
Lo anterior describe brevemente el método para juzgar el rendimiento de las lentes ópticas.
QUANHOM es un fabricante de lentes ópticos personalizados . Nuestro equipo cierra la brecha entre un rendimiento superior y un presupuesto limitado, especialmente cuando participamos en proyectos que integran alta precisión. Los productos incluyen conjuntos ópticos infrarrojos para VIS/SWIR/MWIR/LWIR, oculares, elementos de lentes infrarrojos (desde monoscópicos hasta lentes infrarrojos de cambio rápido entre lentes infrarrojos de campo múltiple y zoom continuo), etc. Nuestros expertos experimentados e inspirados siempre pueden proporcionar IR optimizado. lentes de vidrio y opciones de ensamblaje optomecánico y optoelectrónico.